Упражнения и задачи по теории множеств

1.           Является ли множество всех атомов Солнечной системы бесконечным?

2.           Составить список элементов множеств, заданных посредством характеристического признака:

а) Х={х | };

б) Х={х | };

в) Х={х | хÎN, -4<х£3}.

3.           Описать множества точек М плоскости таких, что:

 а) {М | ОМ=5};

б) {М | ОМ £5};

в) {М | АМ=ВМ}.

4.           Какая разница в записях  АÎВ и АВ?

5.           Равны ли множества {{1, 2}, 3} и {1, 2, 3}?

6.           Верно ли, что {1, 2}Î{{1, 2, 3}, {1, 3}, 1, 2}?

7.           Верно ли, что {1,2} {{1, 2, 3}, {1, 3}, 1, 2}?

8.           Является ли множество {0} пустым?

9.           Доказать, что существует только одно пустое множество.

10.       Привести пример таких множеств А, В, и С, что АÎВ, ВÎС и АС.

11.       Привести пример такого множества В, что для некоторого А одновременно АÎВ и АВ.

12.       Найти  множество-степень P(А)  множества А={1, 2, 3, 4}.

13.       Найти  множество-степень P(А)  множества А={{1, 2}, 3, 4}.

14.       Может ли у множества быть:

а)  0 подмножеств;

б) 7 подмножеств;

в) 16 подмножеств.

15.       Для каждых двух из следующих множеств указать, является ли одно из них подмножеством другого: А={1}, В={1, 2}, С={1, 2, 3}, D={{1}, 2, 3}, E={3, 2, 1}, F={{1, 2}, 3}.

16.       Найти объединение, пересечение, разность и симметрическую разность  множеств А и В, если

а) А={1, 2, 3, 4, 5},  В={2, 4, 6, 8, 10};        б) А={а, б, в, г, д, е}, В={а, в, д, к, и};

в) А={а, в, д, ж, и, м, н, о}, В={в, к, и, о, м, п, с, ф};

г) А={0, 1, 2, 3, 4, 5, 6, 7}, В={3, 4, 5, 6, 7, 8, 9, 10}.

 

17.       Найти объединение, пересечение, разность и симметрическую разность  множеств А и В, если

а) А={а½аÎ(-7; 1]},  В={b½bÎ[-3,4]};         б) А={а½аÎ[-7; 1]},  В={b½bÎ(-3,4)};

в) А={а½аÎ[-7; 1)},  В={b½bÎ[-3,4)};         г) А={а½аÎ(-7; 1)},  В={b½bÎ(-3,4)}.

 

18.       Даны следующие числовые множества: А={1,3,5,7,9,11},  B={2,5,6,11,12}, C={1,2,3,5,9,12}. Найти множества, которые будут получены в результате выполнения следующих операций:

а) (АÈС)DВ;                         б) (АÇС)\В;                                 в) С\BDА;

г) АÇBÇC;                           д) В\(АÇС);                                 е) (BDC)ÈA.

 

19.       Даны следующие числовые множества: А={1,3,5,7,9,11},  B={2,5,6,11,12}, C={1,2,3,5,9,12}. Найти множества, которые будут получены в результате выполнения следующих операций:

а) (АÈС)\(ВDА)\С;                б) (СÈВDА)\(СÇА);                      в) (А\С)È(ВDС);

г) (С\В)È(А\С);                     д) (ВDС)È(А\В) Ç (С\А);              е) (АÇС) D (ВÈА)\С.

 

20.       Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:

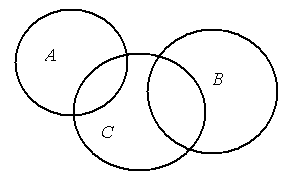
а)  (АÈВ)\С;                          б) (АÇВ)È(СDВ);                          в) (АDВ) Ç (С \ В);

г) (С\В)È(А\С);                      д) (А\С)È(ВDС);                            е) (СDА)\(ВÇА).

 

21.       Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:

а) (А È В) \ (С Ç В);                 б) (А\В)Ç(С \ В);                       в) (С \ А) È (С \ В); 

г) (С \ А) Ç (С \ В);                   д) (С\В)È(А\С);                         е) (АÇС) D (ВÈА)\С.

 

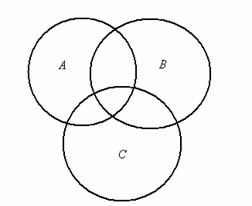
22.       Записать множество, изображенное с помощью кругов Эйлера на рисунке:

                   а)                                         б)                                                 в)

 

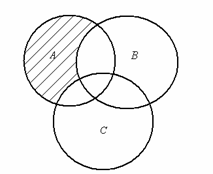
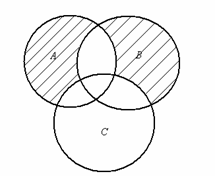
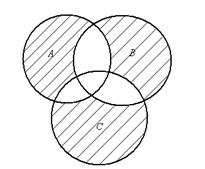
                   г)                                                   д)

 

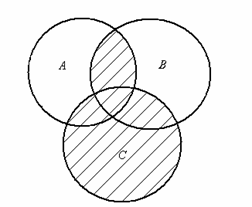
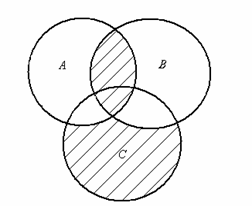
23.             Следует ли из А\В=С утверждение А=ВÈС.

24.             Следует ли из А=ВÈС утверждение С=А\В.

25.             Доказать, что если BA , то АÈВ=А  и  АÇВ=В.

26.             Доказать, что если АÈВ=А, то BA. 

27.             Доказать, что если АÇВ=В, то BA.

28.             Существуют ли такие множества А, В и С, что  АÇВ¹Æ, АÇС=Æ (АÇВ)\С=Æ.

29.             Множество А состоит из натуральных четных чисел, множество В – из натуральных чисел, делящихся на 3. Из каких чисел состоит множество АÇВ?

30.             Множество А состоит из натуральных четных чисел, множество В – из натуральных чисел, делящихся на 3, множество С – из натуральных чисел, делящихся на 12. Из каких чисел состоит множество АÇВÇС? Изобразите множества с помощью кругов Эйлера.

31.             Множество А состоит из натуральных чисел, делящихся на 4, множество В – из натуральных чисел, делящихся на 6, множество С - из натуральных чисел, делящихся на 15. Из каких чисел состоит множество D=АÇВÇС? Изобразите множества с помощью кругов Эйлера.

32.             Старейший математик среди шахматистов и старейший шахматист среди математиков – это один и тот же человек или (возможно) разные?

33.             Лучший математик среди шахматистов и лучший шахматист среди математиков – это один и тот же человек или (возможно) разные?

34.             Каждый десятый математик – шахматист, а каждый пятый шахматист – математик. Кого больше – математиков или шахматистов – и во сколько раз?

35.             Может ли множество двух отцов и двух детей состоять из трех человек? В каком случае?

36.             На окружности выбраны 1000 белых точек и одна черная. Чего больше – треугольников с вершинами в белых точках или четырехугольников, у которых одна вершина черная, а остальные три белые?

37.             Каких подмножеств больше у 100-элементного множества: мощности 57 или мощности 43?

38.             Из 15 спортсменов, занимающихся боксом или борьбой, 10 –  боксеры. Сколько спортсменов занимаются обоими видами спорта, если борьбой занимается 8 из них?

39.             Из 45 курсантов  25 юношей. 30 курсантов учатся на 4 и 5.  28 - занимаются спортом, из них 18 юношей и 17 хорошистов. 15 юношей учатся на 4 и 5 и занимаются спортом. Сколько юношей при этом могут быть хорошистами?

40.             В двух группах учатся 50 курсантов. Для прибытия в институт 12 из них пользуются автобусом, 18 добираются пешком, 7 и идут, и едут в автобусе. Используя теорию множеств, найдите:

·                   Сколько человек или добираются пешком, или пользуются автобусом?

·                   Сколько человек пользуются только автобусом?

·                   Сколько человек пользуются другим транспортом?

41.             На первом курсе в одной группе учатся 40 курсантов. Из них по теории государства и права имеют тройки 19 человек, по информатике и математике - 17 человек и по физкультуре – 22 человека. Только по одному предмету имеют тройки: по теории государства и права – 4 человека, по информатике и математике – 4 человека и по физкультуре  – 11 человек. 7 человек имеют тройки и по информатике и математике, и по физкультуре, из них 5 имеют тройки и по теории государства и права. Сколько человек учится без троек? Сколько человек имеют тройки по двум из трех дисциплин?

42.             Первая рота 1-го курса состоит из 70 курсантов. Из них 27 занимаются в драмкружке, 32 – поют в хоре, 22 – увлекаются спортом. В драмкружке 10 курсантов из хора, в хоре 6 – спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Найти:

·        Сколько курсантов не поют в хоре, не увлекаются спортом и не занимаются в драмкружке?

·        Сколько человек, занимающихся в драмкружке и в хоре, не занимаются спортом?

·        Сколько спортсменов драмкружка не поют в хоре?

·        Сколько поющих спортсменов, не посещающих драмкружок?

·        Сколько спортсменов посещают хор или драмкружок?

·        Сколько увлекаются только спортом?