Основы теории множеств                                                                                                                             

Множество — любая совокупность определенных и различимых между собой объектов, рассматриваемых как единое целое.

Множества обычно обозначают прописными курсивными буквами латинского алфавита: A, B, C и т.д. Объекты, составляющие данное множество, называют его элементами и обозначают строчными курсивными буквами латинского алфавита: а, x, y. Для того, чтобы указать, что x – элемент множества А, записывают   xÎA.

Способы задания множеств:

-        явный или перечислительный (Например, А={понедельник, вторник, среда, четверг, пятница, суббота, воскресенье});

-        описательный (А={a  |  a – день недели}).

Конечным множеством называется множество, состоящее из конечного числа элементов.

Бесконечным называется множество, если оно состоит из бесконечного числа элементов.

Множество, не содержащее элементов вообще, называют пустым и обозначают Æ.

Множество, состоящее из всех рассматриваемых в данном случае элементов, называют универсальным и обозначают I.

Если каждый элемент множества В является также и элементом множества А, то говорят, что множество В называется подмножеством множества А:

В Í А.

 Если множества А и В состоят из одних и тех же элементов, то они называются равными: А=В (интуитивный принцип объемности).

Свойства отношения включения:

·        А  Í А;

·        Æ Í А;

·        А Í I;

·        если АÍВ  и ВÍС, то АÍС   (транзитивность);

·        если АÍВ  и ВÍА, то А=В.      

         Множество А называется истинным подмножеством множества В, если АВ и А≠В:

АÌВ.

Множество всех подмножеств множества А называется множеством-степенью множества А.

 

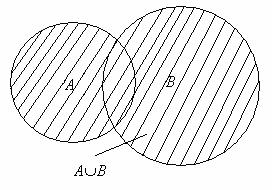
 Объединением множеств А и В называется множество С, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В, т. е. принадлежат А, или принадлежат В, или принадлежат и А и В:

С=АÈВ={cïcÎA  или сÎВ}.

Свойства операции объединения:

1)           АÈВ = ВÈА  –  коммутативность (переместительность);

2)           (АÈВ)ÈС = АÈ(ВÈС)  –  ассоциативность (сочетательность)

3)           (АÇВ) È С = (АÈС) Ç (ВÈС)  – дистрибутивность (распределительность).

4)           АÈА = А      –  закон  идемпотентности;

5)           если АÍВ, то АÈВ = В.

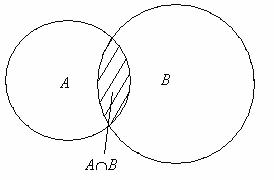
Пересечением множеств А и В называется множество С, состоящее из элементов, которые принадлежат как множеству А, так и множеству В одновременно:

С=АÇВ={cïcÎA  и  сÎВ}.

 Свойства операции пересечения:

1)           АÇВ =  ВÇА  –  коммутативность (переместительность);

2)           (АÇВ)ÇС = АÇ(ВÇС)  –  ассоциативность (сочетательность);

3)           (АÈВ) ÇС = (АÇС) È (ВÇС)  – дистрибутивность (распределительность).

4)           АÇА=А       –   идемпотентность;

5)           если АÍВ, то АÇВ=А.

 

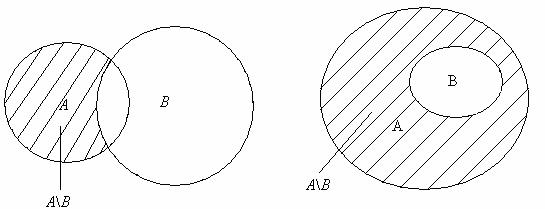
Разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат множеству А, но не входят в множество В:

С=А\В={cïcÎA  и  сÏВ}.

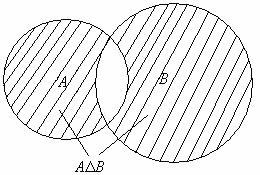
Симметрической разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат какому-то одному из множеств А или В:

С=АDВ= (А\В)È (В\А).

Свойства симметрической разности множеств:

1)      АDВ =  ВDА  –  коммутативность (переместительность);

2)     (АDВ)DС = АD(ВDС)  –  ассоциативность (сочетательность);

3)     (АDВ)ÇС = (АÇС) D (ВÇС)  – дистрибутивность (распределительность).

 

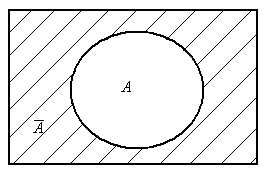
       Разность I\А называется дополнением множества А до множества I или просто дополнением множества А и обозначается .

1)           =А;

2)           = I ,                      = Æ;

3)           ,    – законы де Моргана;

4)           АÈ(АÇB)=А,    АÇ(АÈB)=А – законы поглощения;

5)           АÇ = Æ,            АÈ = I ;

6)           АÈÆ = А,             АÇI  = А;     

7)           АÇÆ = Æ,            АÈI  = I .

Число элементов конечного множества будем обозначать через N(A).  Для двух конечных множества А и В, количество элементов которых N(A) и N(В),

N(АÈВ)= N(A)+N(В) –N(АÇВ)

(формула включений и исключений).

         Формула включений и исключений для трех конечных множеств А , В и С:

N(A) + N(В) + N(С) – N(АÇВ) – N(BÇC) – N(АÇC) + N(АÇВÇC).

                                              

N(I) – N(А).

 

Если два конечных множества А и В имеют одинаковое количество элементов, то они называются равночисленными.