1. Записать в виде логических формул высказывания:
a) Если преступление предусмотрено общей
и специальной нормами, совокупность преступлений отсутствует и уголовная
ответственность наступает по специальной норме. Статья 17 УК РФ.
b) Преступление признается совершенным с
прямым умыслом, если лицо осознавало общественную опасность своих действий
(бездействия), предвидело возможность или неизбежность наступления общественно
опасных последствий и желало их наступления. Статья 25 УК РФ.
c) Преступление признается совершенным
группой лиц, если в его совершении совместно участвовали два или более
исполнителя без предварительного сговора. Статья 35 УК РФ.
2. Пусть А -
истинное высказывание, В - ложное
высказывание. Определить значение истинности следующих сложных высказываний:
a)
(AÚ B)® A ;
b)
(A
Ù B) ® A;
c)
A « (A Ù B) ® A;
d)
A ® (B « A);
e)
® 
;
f)
;
g)
(A
Ù )
® B;
h)
(A
« (B Ú 
)) ® ;
i)
A Ú B ®Ù (A ®B);
j)
A Ù (® AÚ B);
k)
A « (B ® Ú (A «);
l)
(AÚ B) ® (B Ù );
m)
(® B) ® (Ù
;
n)
A « (® A) Ú (A® ));
o) (A Ú) Ù (Ú B) « .
3. Построить таблицу
истинности логических формул:
a)
A Ù (« AÚB);
b)
® (AÚ);
c)
A Ú (B « B Ú);
d)
AÚB ® Ù (A «B);
e)
Ù B Ú ( « AÚ );
f)
Ú (Ù B) « ;
g)
B Ú Ù (B Ù A ® );
h)
A Ú B « ( Ù ® B);
i)
A « (AÚ ® Ù );
j)
(B
® Ú ( A Ù B)) « AÚ B;
k)
® (C Ú );
l)
A Ú (B ® C Ú );
m)
A Ú ® (
Ù ) « ;
n)
A « (B ® C Ù );
o) « (B Ú (C ®)).
4. Проверить, является ли логическая формула тавтологией:
a)
(B
® (AÚ )) Ù (A ® (B Ú ));
b)
(A
Ú B)
® (B Ú );
c)
A « (A Ú ) Ù ;
d)
A ® (A Ú ( Ù A));
e)
A ®
((B Ù ) ® A);
f)
(A
® B) ® AÚ B « 
;
g)
AÚ B «;
h)
(Ú B ® B) « AÚ B;
i)
(Ú B ® A) « A ÙB;
j)
Ú ( ® );
k)
Ù;
l)
A Ù ® (AÚ B « );
m)
A Ú ® (Ù ) « ;
n)
A « (B ®A Ù );
o) « (B Ú (A ® )).
5. Известно, что импликация A ® B истинна, а
эквивалентность A «B ложна. Что
можно сказать о значении импликации B ® A?
6. Найти логические значения A и B,
при которых выполнятся равенства:
a)
(1 ® A) ® B = 0,
b)
A Ú B = .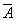
7. Найти равносильную
формулу операции эквивалентность, в которой используются:
a) только три операции: отрицания,
дизъюнкции и конъюнкции;
b) только две операции: отрицания и
дизъюнкции.
8. Выразить операции дизъюнкции, конъюнкции
и эквивалентности через отрицание и
импликацию. АÚВº
; АÙВº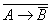
; A«Bº(A®B)Ù(B®A).
9.
Доказать закон контрапозиции и Modus ponens с помощью таблиц истинности.
10. Проверить правильность
рассуждения средствами логики суждений: "Если человек осуждён судом, то он
лишается избирательных прав. Если человек признан невменяемым, то он также
лишается избирательных прав. Следовательно, если человек обладает избирательным
правом, то он здоров и не был осуждён судом".
11. Проверить
правильность рассуждения средствами логики суждений: «Иванов утверждает, что не встречал этой ночью Сидорова.
Если Иванов не встречал этой ночью Сидорова, то либо Сидоров был убийцей, либо Иванов
лжёт. Если Сидоров не был убийцей, то Иванов не встречал его этой ночью, а убийство
было совершено после полуночи. Если убийство было совершено после полуночи, то либо
Сидоров был убийцей, либо Иванов лжёт. Следовательно, убийцей был Сидоров».
12. Проверить
правильность рассуждения средствами логики суждений: «Если бы он не пошёл в кино,
то он не получил бы двойки. Если бы он подготовил домашнее задание, то не пошёл
бы в кино. Он получил двойку. Значит, он не подготовил домашнее задание».
13. Проверить правильность следующего
рассуждения: «Для того чтобы сдать экзамен, мне необходимо достать учебник или
конспект. Я достану конспект только в том случае, если мой приятель не уедет.
Мой приятель уедет, только если я сдам экзамен. Следовательно, я сдам экзамен».
14. Выяснить, кто из четверых виновен на
основе информации: “Петров виновен, только если виновен Иванов. Неверно, что
виновность Сидорова влечет виновность Родионова и что Иванов виновен, а Сидоров
нет”.
15. Петров, Иванов и Сидоров сдавали
экзамен по информатике и математике. Если Петров не сдал экзамен на «отлично»,
то и Иванов не сдал на «отлично». Сидоров и еще один из друзей сдали экзамен на
«отлично». Следует ли отсюда, что не
верно, что Петров сдал экзамен не на «отлично», а Иванов на «отлично»?
16. На складе совершено хищение.
Подозрение пало на трех человек: a, b, и c, они были доставлены для допроса. Установлено
следующее:
·
Никто,
кроме a, b, c, не был замешан в деле.
·
a никогда не ходит на дело без, по
крайней мере, одного соучастника.
·
c не виновен.
Виновен ли b?
17. Разбирается дело Иванова, Петрова и
Сидорова. Один из них совершил преступление. В процессе расследования каждый из
них сделал по два заявления.
Иванов: Я не делал этого. Петров не делал
этого.
Петров: Сидоров сделал это. Иванов не
делал этого.
Сидоров: Я не делал это. Иванов
сделал это.
Далее было установлено, что один из них дважды солгал, другой
дважды сказал правду, а третий раз солгал, раз сказал правду.
Кто совершил преступление? Какой будет ответ при условии, что
каждый из них один раз сказал правду, а один раз солгал?
18. В деле об убийстве имеются двое
подозреваемых - Иванов и Петров. Допросили четырех свидетелей, которые
последовательно дали такие показания: "Иванов не виноват",
"Петров не виноват", "Из двух первых показаний по меньше мере
одно истинно", "Показания третьего ложны". Четвертый свидетель
оказался прав. Кто виновен?
19. По подозрению в совершенном
преступлении задержали Иванова, Петрова и Сидорова. Один из них был уважаемым в
городе стариком, другой был малоизвестным чиновником, третий - известным
мошенником. В процессе следствия старик говорил правду, мошенник лгал, а третий
задержанный в одном случае говорил правду, а в другом - ложь. Вот, что они утверждали:
Иванов: Я совершил это. Петров не виноват.
Петров: Иванов не виноват.
Преступление совершил Сидоров.
Сидоров: Я не виноват. Виноват
Иванов.
Требуется определить фамилии старика,
мошенника и чиновника, и кто из них виноват, если известно, что преступник
один.
20. В Советском районе города
Ростова-на-Дону было совершено ограбление
квартиры. Подозрение пало на двух известных воров Иванова и Петрова. Кроме
того, обнаружились три свидетеля, которые заявили:
Первый: Это они сделали вместе.
Второй: Ограбление совершил Иванов, Петров в
этом не участвовал.
Третий: Если Петров совершил ограбление, то
Иванов тоже принимал в этом участие.
Какой вывод
можно сделать из показаний свидетелей, если выяснилось, что все они врали?
21. Предположим, что а говорит: "Или я
лжец, или b рыцарь". Кто из двух персонажей
– а
и b – рыцарь и кто лжец?
22. Предположим, что а высказывает
утверждение: "Я – лжец, а b не лжец". Кто из персонажей а
и b рыцарь и кто лжец?
23. Предположим, а утверждает: «Если b рыцарь, то я – лжец». Кто из персонажей
а
и b рыцарь и кто лжец?
24. Предположим, а утверждает: «Если я
рыцарь, то и b – рыцарь». Убедиться, что и а и b – рыцари.
25. Известно, что каждый из а,
b, с
является либо рыцарем, либо лжецом. Можно ли определить, кто есть кто, по их следующим
высказываниям:
а: « Мы все рыцари»;
b: «Только один из нас – рыцари»?
26. На некотором острове, населенном
рыцарями и лжецами, разнесся слух о том, что на нем зарыты сокровища. Вы
прибываете на остров и спрашиваете одного из местных жителей: “Есть ли на
острове золото?”. В ответ на ваш вопрос он заявляет: “Сокровища на этом острове
есть в том и только в том случае, если я рыцарь”.
а) можно ли определить, кто такой этот местный - рыцарь или
лжец?
б) можно ли определить, есть ли сокровища на острове?
27. Один из а, b и с является рыцарем, один
лжецом, один – нормальным человеком[1]. Они
утверждают следующее:
а: « Я нормальный человек»;
b: « То, что сказал А, - правда»;
с: « Я – не нормальный человек».
Кем являются а, b и с в действительности?